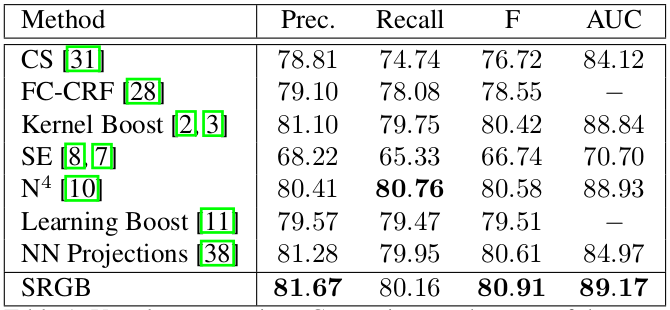
We propose a new way to train a structured output prediction model. More specifically, we train nonlocal data terms in a Gaussian Conditional Random Field (GCRF) by a generalized version of gradient boosting. The approach is evaluated on three challenging regression benchmarks: vessel detection, single image depth estimation and image inpainting. These experiments suggest that the proposed boosting framework matches or exceeds the state-of-the-art.

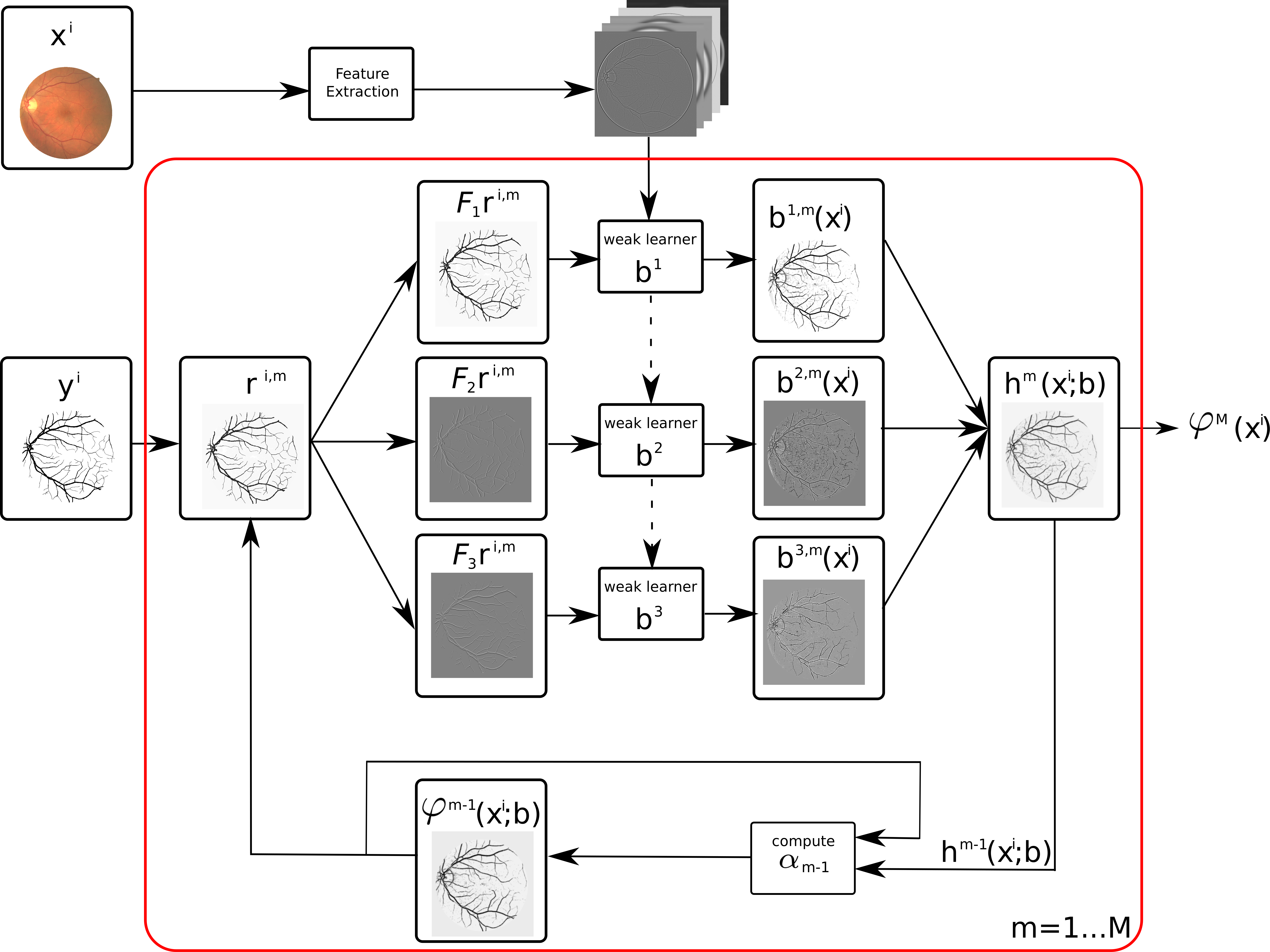Structured regression gradient boosting. Given input \(x^i\)and structured ground truth \(\mathrm{y}^i\), we iterate the following: given the current prediction \(\varphi^{m-1}(\mathrm{x}^i)\), compute gradient \(\mathrm{r}^{i,m}\) of the structured loss. Next, train shallow regression trees that produce good fits \(\mathrm{b}^{k,m}\) to the structured loss gradient image and filtered versions thereof. Use these fits to parametrize the data terms of a Gaussian conditional random field. Its MAP solution \(\mathrm{h}^m(\mathrm{x}^i)\) is added to the current strong structured learner with a weight \(\alpha_m\) found through line search. Repeat \(M\) times.

A helpful video of the temporal evolution of the prediction and the negative gradient direction at each iteration is shown below.

Temporal evolution of the prediction

Learned negative gradient direction

Results for the DRIVE dataset [40] in the form of the recall/precision curves. Our approach is slightly above the performance of the current state-of-the-art methods by \(N^4\)-Fields [10], Kernel Boost [3] and NN Projections [38], and much better than [8] and [31].

Comparison to the state of the art on the DRIVE dataset.

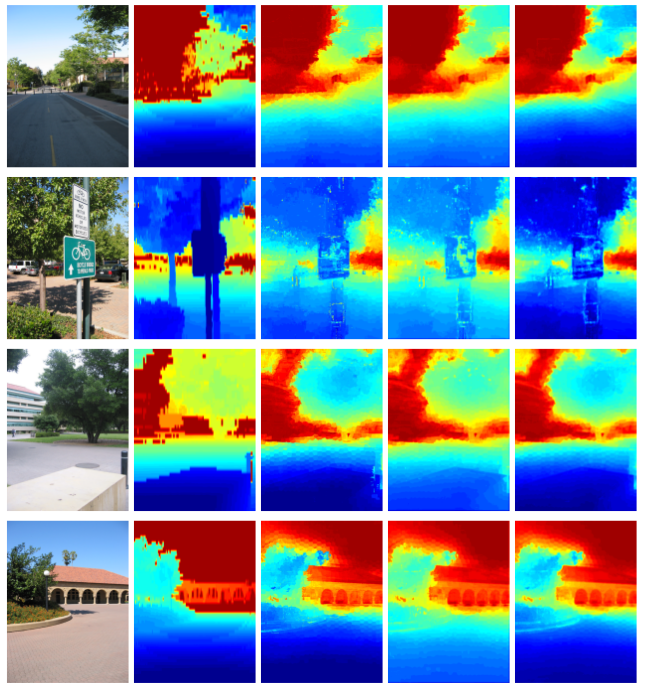Examples of depth predictions on the Make3D dataset. From left to right: original image, ground truth, gradient boosting baseline ($K=1$), our gradient boosting with pairwise connectivity ($K=3$) and our approach with pairwise connectivity and with the data term computed from a fully connected 5$\times$5 neighborhood ($K=27$). The gradient boosting gives rather coarse prediction mainly due to the coarse depth estimations used as features. In contrast, our full model yields much better predictions.

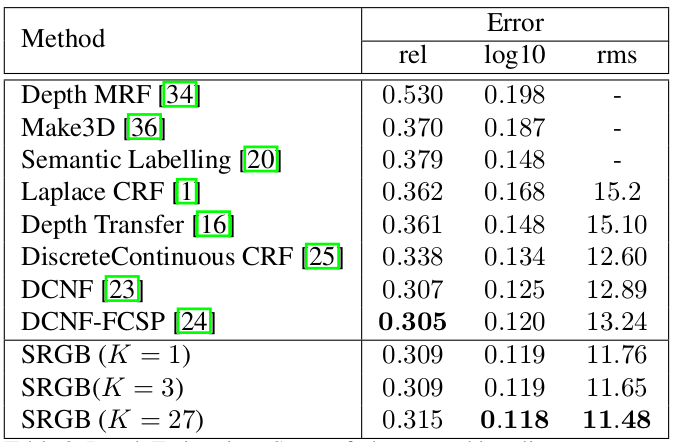State-of-the-art and baseline comparisons on the Make3D dataset.

Chinese characters with large occlusions: inpainting result on test set. All the characters are also shown in [14, Fig. 7].

Accuracy for inpainting of small occlusions.